“西海 学缺
学缺
 才,
才,
 里也
里也 更受
更受 视……”
视……”
然 林伯涵来了。
林伯涵来了。
 浩
浩 林伯涵确实非常
林伯涵确实非常 视。
视。
林伯涵正式 职
职
 ,
,
 拉
拉
 方一起
方一起 研究,“林博士,
研究,“林博士, 来
来 正
正 !”
!”
“ 正
正 为研究
为研究 疼。”
疼。”
 拉
拉 林伯涵
林伯涵 了起来,“
了起来,“ 正
正 研究一
研究一 ,类似
,类似 微观形态
微观形态
 何
何 题,
题,
 微观形态,经过拓扑
微观形态,经过拓扑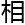 变
变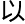
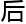 ,就
,就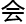 形成
形成 维无限延展
维无限延展 形状……”
形状……”
 浩仔细
浩仔细 了起来。
了起来。
 导
导
 微观形态
微观形态
 象,就
象,就
 一
一
 规则
规则 球
球 ,球
,球

 侧
侧 打通
打通 。
。
 象
象 ,微观形态
,微观形态
 特殊球
特殊球 ,
,
 真正结构并非
真正结构并非 此,
此, 须
须
 足
足
 求。
求。
一
 经过挤压
经过挤压
 ,
, 逸散
逸散
 包裹
包裹 ‘特殊力场’,或者
‘特殊力场’,或者 影响
影响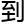

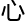 通
通
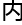
 微观运用,近
微观运用,近 形成
形成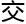
 力作用。
力作用。


 拓扑形态,
拓扑形态, 无限延伸
无限延伸
 维圆筒式平面,
维圆筒式平面, 维圆筒也
维圆筒也
 完善
完善 ,
, 间
间
 现一些孔
现一些孔 ,圆筒
,圆筒

 影响
影响 微观运动。
微观运动。
 特殊球
特殊球 表面
表面 意
意 条
条 线都
线都
 ,
,
 拓扑形态,
拓扑形态, 何
何 条
条 线都
线都 平
平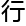
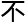

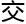
 。
。
最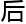 一
一 才
才 最难
最难 足
足 ,研究也牵扯
,研究也牵扯 复杂
复杂 何
何 析。
析。
 特殊
特殊
 何
何 求,和导
求,和导
 微观形态
微观形态
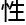 质
质 接
接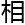 关。
关。
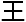 浩
浩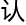 为导
为导
 微观形态和电磁力
微观形态和电磁力 接
接 关,或者
关,或者
 ,微观形态决定了电磁受力。
,微观形态决定了电磁受力。
 超导
超导 特殊状态
特殊状态 ,微观形态拓扑化,就导致了超导状态
,微观形态拓扑化,就导致了超导状态 导
导 ,
,
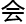
 受
受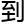 电磁力
电磁力 影响(
影响(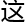

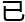 经证实
经证实 )。
)。
另外,微观形态和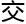
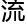
 力场存
力场存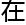
 接关系,有些微观形态更完善,拓扑化
接关系,有些微观形态更完善,拓扑化 难度更
难度更 ,也就表示激活超导状态
,也就表示激活超导状态
 求(温度)更
求(温度)更 。
。
反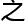 ,则
,则
 温超导材料。
温超导材料。
林伯涵听了 浩
浩
 法,顿
法,顿
 觉有些
觉有些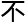
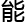 理解,“拓扑
理解,“拓扑 概念里,
概念里,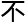 存
存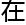
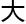 小
小 概念,无限延伸
概念,无限延伸
 维筒状平面,应该
维筒状平面,应该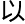
 何方
何方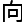
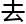 讨论。”
讨论。”
“或许也
 理解为‘定
理解为‘定 拓扑’?”
拓扑’?”
“

 研究拓扑
研究拓扑 原形态,
原形态,
 创造一
创造一 全
全

 何空间……”
何空间……”
林伯涵 了起来,
了起来,
 主方
主方

 何拓扑,
何拓扑,
 欧氏
欧氏 何、黎曼
何、黎曼 何都有一定
何都有一定 涉猎,“
涉猎,“

 创造一
创造一 全
全

 何空间,定义
何空间,定义 就
就 更严谨一些。”
更严谨一些。”
 浩
浩
 ,“一
,“一 特定
特定
 维
维 何空间,
何空间,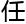 何
何 条
条 线都
线都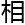
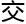 ,
, 怎
怎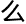
 理解?”
理解?”
“
 简单!”
简单!”
林伯涵写 定义
定义 了
了 图形,随
图形,随

 就一起讨论起来。
就一起讨论起来。
……
 据研究
据研究 实际需
实际需 ,
,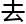 定义一
定义一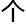
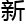

 何空间,确实
何空间,确实 非常有意思
非常有意思 工作。
工作。
 何,并
何,并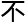
 固定
固定 。
。
 小学教材
小学教材

 何定理,也
何定理,也
 基础
基础
 基础
基础
 ,真正
,真正
 何学
何学 领域,一切常规定义和公理,就都成了一项普通
领域,一切常规定义和公理,就都成了一项普通 基础定义。
基础定义。
 ,
,
 黎曼
黎曼 何。
何。
黎曼 何
何 一
一 基础定义
基础定义 ,
,
 一平面
一平面
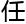 何
何 条
条 线都有公共
线都有公共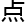 (
(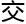
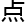 )。
)。
 黎曼
黎曼 何学
何学
 承
承 平
平 线
线 存
存 ,
,
 另一条公设
另一条公设

 ,
, 线
线
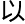 无限延
无限延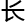 ,
,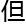
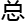

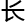 度
度 有限
有限 。
。
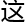 些定义显然违背常理。
些定义显然违背常理。
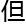 黎曼
黎曼 何却
何却 广义
广义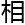
 论
论 数学基础,
数学基础,
 ,黎曼
,黎曼 何也
何也 数学
数学


 工
工 ,
,
 仅
仅 微
微
 何
何 基础,也应用
基础,也应用 微
微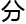 方程、变
方程、变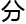 法和复变函数论等方面。
法和复变函数论等方面。
现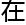 林伯涵和
林伯涵和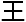 浩所
浩所
 工作,则
工作,则 试
试
 定义一
定义一

 何空间,
何空间, 便让
便让
 足研究需求。
足研究需求。
下载app进行无广告阅读!