每当


 邱
邱 安,丁志
安,丁志 也希望真
也希望真 研究
研究
 东西。
东西。
当研究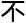 断
断
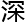
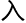
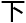
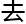 ,邱
,邱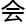 安
安
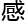 觉就
觉就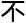 怎
怎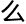
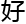 了,
了,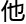 一
一 都
都 研究
研究 参
参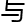 者,
者, 来就发现
来就发现 难跟
难跟 节奏。
节奏。
最

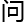 题
题 ,讨论
,讨论 方
方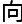 主
主 放
放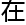 代数
代数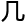 何、函数
何、函数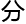 析
析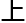 。
。
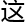 方面,
方面,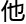 没有优势。
没有优势。
所
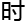 间里,
间里,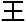 浩都
浩都 和丁志
和丁志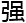 讨论,
讨论,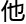 就
就
 跟
跟 旁听
旁听 句。
句。
 研究有了
研究有了 展。
展。
 浩和丁志
浩和丁志 讨论
讨论 '红线
'红线 应复平面和黎曼猜
应复平面和黎曼猜
 关系',谈
关系',谈 了包
了包
 被包
被包
 关系',丁志
关系',丁志
 为关系
为关系
 现
现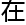 所
所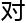 应
应 '质数
'质数 '
'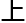 ,
,
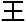 浩则
浩则 得
得 了确定
了确定 结论—
结论—
红线所 应
应 复平面,包
复平面,包 黎曼ζ函数
黎曼ζ函数 所有非平凡
所有非平凡
 。
。

 红线所
红线所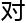 应
应 复平面,作为一
复平面,作为一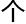
 位
位 集合a,黎曼ζ函数
集合a,黎曼ζ函数 所有非平凡
所有非平凡
 为集合b,
为集合b, 者
者 关系就
关系就 anb=b(
anb=b(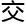 集),也就
集),也就 a
a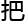 b全
b全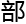 包
包
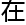
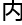 。
。
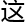
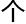 发现似乎
发现似乎
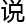
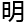 了
了 者
者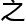 间
间 关系,
关系, 实际
实际 ,灵
,灵 值
值 提升
提升 了'23'
了'23' ,因为结论
,因为结论 通过系统反馈得
通过系统反馈得
 ,并没有完善
,并没有完善 证
证 过程。
过程。
 有了确定
有了确定 结论,针
结论,针 结论
结论 寻找方
寻找方 ,
,
 就容易了许
就容易了许 。
。
从灵 数值就
数值就
 ,距离完成研究还有
,距离完成研究还有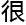 远,主
远,主 难
难 就
就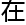
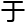 函数难
函数难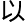 解析,另外,红线所
解析,另外,红线所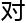 应
应 复平面,
复平面,
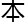 无法用一
无法用一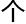 函数方程来表达。
函数方程来表达。
就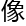
 邱
邱 安
安 理解,复平面
理解,复平面 无数
无数
 维图形
维图形
 线,
线,

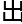 表达就
表达就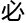 须
须 联系所有
联系所有
 维图形,
维图形,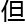 图形
图形 数量
数量 无穷
无穷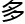
 。
。
 一
一
 展
展 现
现

 。
。
 次
次
 浩找
浩找 了关键,
了关键, 发现联系黎曼函数
发现联系黎曼函数 让研究变得极为复杂,就
让研究变得极为复杂,就 脆排除了黎曼函数
脆排除了黎曼函数 影响,结
影响,结 有了
有了

 法。
法。
「或许,最小 接
接 函数
函数 所有质数
所有质数 位,都
位,都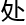
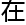
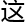
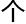 平面
平面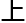 ?」
?」
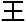 浩最
浩最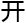 始
始
 一
一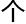
 法,和丁志
法,和丁志 讨论了一阵,顿
讨论了一阵,顿 确定了结论,反应
确定了结论,反应 系统
系统 务
务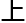 ,灵
,灵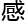 值迅速提升了'17'
值迅速提升了'17' 。
。
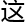
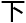 研究
研究
 方
方
 确
确 。
。
 尔卡尔终
尔卡尔终 回来了。
回来了。
 回
回 了西海
了西海 学
学
 ,就来了一趟梅森数科学
,就来了一趟梅森数科学
 ,和熟悉
,和熟悉
 打听了一
打听了一
 浩
浩 研究。
研究。
 浩和丁志
浩和丁志 、邱
、邱 安一起
安一起 研究并没有保密,
研究并没有保密, 因为
因为 纯数学
纯数学
 容,其
容,其
 也没有参
也没有参
 来,
来,
 研究
研究 容
容
 有
有 模糊
模糊
 。
。
「
 和黎曼猜
和黎曼猜 有关。」—张志
有关。」—张志 。
。
「代数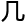 何、黎曼猜
何、黎曼猜 ,似乎
,似乎
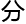 析
析 者
者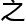 间
间 关系?
关系?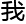 听陈蒙檬
听陈蒙檬 过
过 句。」—罗
句。」—罗 勇。
勇。
「 照罗
照罗 勇
勇
 ,
,
 和霍奇猜
和霍奇猜 有关系?
有关系?
 清楚」—田虹。
清楚」—田虹。
 尔卡尔一脸迷茫。
尔卡尔一脸迷茫。
下载app进行无广告阅读!